test
test test
Giáo dục định hướng Đạo đức
Nói về giáo dục đạo đức, cũng là nói đến một vấn đề rất cổ xưa. Nó xưa tới mức độ nào? Căn cứ trên các tư liệu lịch sử, có thể thấy rằng giáo dục đạo đức đã xuất hiện từ rất lâu, trước khi nền văn minh này xuất hiện, thậm chí còn lâu hơn nữa. Mặc dù vậy, nó cũng là một chủ đề xuyên suốt lịch sử, nhất là trong xã hội hiện đại hiện nay. Khi mà những tiến bộ khoa học kỹ thuật thể hiện ra những mặt trái, người ta có thể mường tượng đến những ảnh hưởng bất lợi của chúng đến sự sống còn của con người khi không có sự ước chế về đạo đức. Do đó, có thể có thêm những xu hướng, định hướng giáo dục khác nhau ở từng giai đoạn khác nhau của xã hội, nhưng định hướng giáo dục đạo đức vẫn luôn là quan trọng nhất, cốt yếu nhất, giá trị nhất.
(more…)Tính chất ba đường trung tuyến
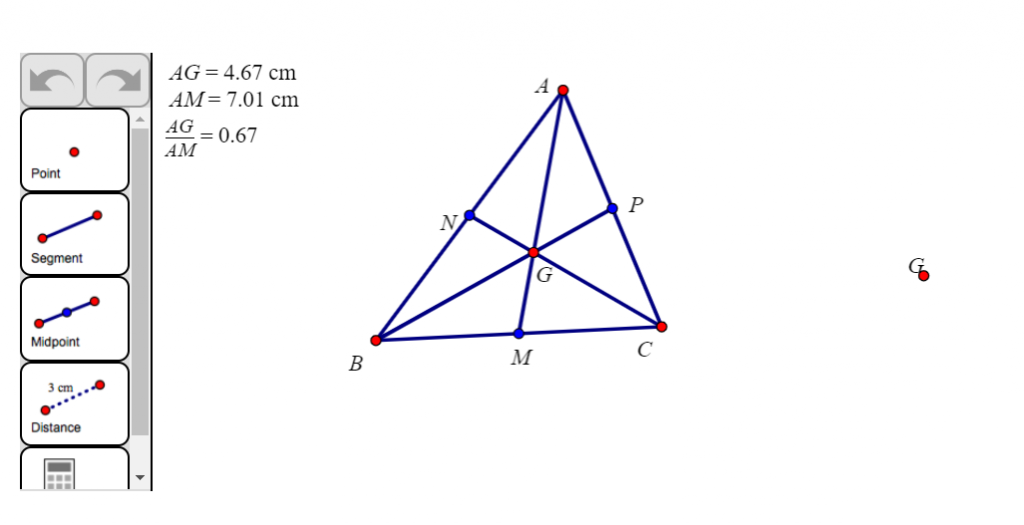
- Đường trung tuyến của tam giác là đoạn thẳng có một đầu là đỉnh của tam giác đầu kia là trung điểm của cạnh đối diện với đỉnh đó.
- Mỗi tam giác có ba đường trung tuyến.
- Định lý: Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng
2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
- Giao điểm của ba đường trung tuyến gọi là trọng tâm.
Định lý sin trong tam giác
Giải tam giác : Giải tam giác là đi tìm các yếu tố (góc, cạnh) chưa biết của tam giác khi đã biết một số yếu tố của tam giác đó.
Muốn giải tam giác ta cần tìm mối liên hệ giữa các góc, cạnh đã cho với các góc, các cạnh chưa biết của tam giác thông qua các hệ thức đã được nêu trong định lí cosin, định lí sin và các công thức tính diện tích tam giác.
(more…)Tạo và in cái bình qua việc xây dựng mặt tròn xoay từ 5 điểm
Trong mặt phẳng \(Oxy\), cho trước 5 điểm \(A, B, C, D, E\). Trong tình huống thông thường, chúng ta có thể tạo một đường cong có phương trình dạng đa thức bậc 4 đi qua 5 điểm này. Từ một phần của đường cong liên quan tới 5 điểm, ta có thể dựng một mặt tròn xoay bằng cách xoay phần đường cong đó quanh một trục. Ví dụ sau đây có thể giúp chúng ta tạo một cái bình (Vase) từ 5 điểm như vậy, và nếu có máy in 3D, quý vị có thể in cái bình này.
Tích hợp Web Sketchpad trong các khóa học trực tuyến trên Moodle
Web Sketchpad (WSP) là một công nghệ mới do McGraw-Hill Education sản xuất và có nguồn gốc từ The Geometer’s Sketchpad. WSP hỗ trợ giao diện người dùng đơn giản nhưng mạnh mẽ bằng cách cung cấp cho nhà thiết kế các hoạt động giáo dục toán các công cụ dễ sử dụng và nhắm mục tiêu chính xác đến một hoạt động học toán cụ thể. Các mô hình tạo ra từ WSP tương thích với bất kỳ trình duyệt web hiện đại nào, không yêu cầu phần mềm hoặc giấy phép khác. Hãy thử khám phá mô hình dưới đây:
Cách viết câu hỏi TNKQ từ bài toán tự luận
Giả sử chúng ta đang cần viết một hay nhiều câu hỏi để đánh giá khả năng toán của học sinh trong một tình huống cụ thể là sử dụng định lý sin. Trong một kỳ thi thông thường, điều này có thể được làm tốt bằng cách dùng công cụ câu hỏi sau:
Tài liệu Module 3: Kiểm tra đánh giá học sinh THCS, THPT theo hướng phát triển phẩm chất và năng lực môn Toán
Mô đun kiểm tra, đánh giá HS TH theo hướng phát triển phẩm chất, năng lực HS là Mô đun bồi dưỡng GV phổ thông cốt cán trong việc thực hiện đổi mới kiểm tra, đánh giá kết quả học tập, rèn luyện của học HS theo yêu cầu của chương trình giáo dục phổ thông 2018.
Mô đun này được xây dựng theo cấu trúc tích hợp giữa lý thuyết và thực hành, nhằm nâng cao hiểu biết cho học viên những kiến thức cơ bản về kiểm tra, đánh giá HS theo hướng phát triển phẩm chất và năng lực, trên cơ sở đó, học viên sẽ được phát triển kỹ năng sử dụng các công cụ đánh giá để phát triển phẩm chất, năng lực HS trong quá trình dạy học môn học.
(more…)Tài liệu về phương pháp giáo dục phẩm chất & năng lực môn Toán
Mô đun 2 “Sử dụng phương pháp dạy học và giáo dục phát triển phẩm chất, năng lực học sinh trung học cơ sở môn Toán” được triển khai nhằm bồi dưỡng, nâng cao năng lực lựa chọn và sử dụng PP, KTDH phát triển phẩm chất, năng lực của HS cho GV môn Toán ở THCS. Hoàn thành mô đun này, không những GV tổ chức được hoạt động dạy học môn Toán theo các yêu cầu của CT GDPT 2018 mà còn đáp ứng được các tiêu chí của tiêu chuẩn Phát triển chuyên môn, nghiệp vụ đối với GV theo Thông tư số 20/2018/TT- BGDĐT, ngày 22/8/2018 của Bộ Trưởng Bộ Giáo dục và Đào tạo về việc ban hành quy định Chuẩn nghề nghiệp GV cơ sở GDPT.